Supervised learning#
Classification for proteins based on sequence information is an important tool for their functional annotation. Supervised machine learning algorithms are a lucrative option to develop classification models. Starting with a set to protein sequences that belong to a particular class (positive dataset) and a set of protein sequences that do not belong to that particular class (negative dataset), machines learning model is built to classify unknown protein sequences. The model trains itself based on certain set of “features” that represent the different sequences in the two datasets.
Datasets#
The first step for any supervised machine learning execise is to prepare a dataset having positive and negative cases. In our case we’ll need a set of protein sequences that would represent positive and negative classes. We know that proteins are polymers made of 20 different amino acids. Proteins have been classified into different families based on their sequence similarity. For practice, we’ll use some of the datasets that are available in the literature. Below are two such datasets correponding to two different binary classification model building.
Feature extraction#
The next and one of the most important step in machine learning is feature extraction. For classifcation of protein sequences we cannot input the amino acid sequence directly to the classifier. The reason for that is because the protein sequences, even if from same family, can have different length. So, we need to transform our data such that each sequence can be represent as a feature of constant length. Amino acid composition is one of the feature that can be used in this senario. Amino Acid Composition refers to frequency of each amino acid within a protein sequence. E.g. if a protein has a sequence ‘MSAARQTTRKAE’ it’s amino acid composition can be represented as a vector of length 20:
‘A’:3,’C’:0,’D’:0,’E’:1,’F’:0,’G’:0,’H’:0,’I’:0,’K’:1,’L’:0,’M’:1,’N’:0,’P’:0,’Q’:1,’R’:1,’S’:1,’T’:2,’V’:0,’W’:0,’Y’:0
In this way any protein sequence can be represented as a feature vector of fixed length. This is important because the protein sequences, even within the same class, can have different number of amino acids. To start with feature extraction and model building, we’ll import the required libraries.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from Bio import SeqIO
from Bio.SeqUtils.ProtParam import ProteinAnalysis
from sklearn import model_selection
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
First, we’ll use SeqIO.parse function to read the sequence files and make a dictionary of all the sequences using the to_dict function. This dictionary would have fasta header as the keys of the dictionary and the sequence object as the corresponding values. Then, using the get_amino_acids_percent function from the Biopython library, the amino acid composition for all the sequences will be calculated. The code below shows the output for this function using a dummy sequence.
p1 = ProteinAnalysis("AAAASTRRRTRRAWEQWERQW")
p1.get_amino_acids_percent()
{'A': 0.23809523809523808,
'C': 0.0,
'D': 0.0,
'E': 0.09523809523809523,
'F': 0.0,
'G': 0.0,
'H': 0.0,
'I': 0.0,
'K': 0.0,
'L': 0.0,
'M': 0.0,
'N': 0.0,
'P': 0.0,
'Q': 0.09523809523809523,
'R': 0.2857142857142857,
'S': 0.047619047619047616,
'T': 0.09523809523809523,
'V': 0.0,
'W': 0.14285714285714285,
'Y': 0.0}
The code below creates the two dataframes one each for the positive and negative datasets. We’ll add labels (as indicies) 1 and -1 to indicate positive and negative classes, respectively.
positive_dict = SeqIO.to_dict(SeqIO.parse("positive-aars.fasta", "fasta"))
for x,y in positive_dict.items():
# print(x)
# print(y.seq)
p1 = ProteinAnalysis(y.seq)
# print(p1.get_amino_acids_percent())
# display(pd.Series(p1.get_amino_acids_percent(), name="1").to_frame().T)
positive_dict = SeqIO.to_dict(SeqIO.parse("positive-aars.fasta", "fasta"))
negative_dict = SeqIO.to_dict(SeqIO.parse("negative-aars.fasta", "fasta"))
## Amino acid composition calculation##
#c1 = ProteinAnalysis("AAAASTRRRTRRAWEQWERQW").count_amino_acids()
df1 = pd.DataFrame()
for keys,values in positive_dict.items():
df1 = pd.concat([df1, pd.Series(ProteinAnalysis(str(values.seq)).get_amino_acids_percent(),name='1').to_frame().T])
for keys,values in negative_dict.items():
df1 = pd.concat([df1, pd.Series(ProteinAnalysis(str(values.seq)).get_amino_acids_percent(),name='-1').to_frame().T])
print("Number of positive samples: ", len(positive_dict))
print("Number of negative samples: ", len(negative_dict))
df1
Number of positive samples: 117
Number of negative samples: 117
| A | C | D | E | F | G | H | I | K | L | M | N | P | Q | R | S | T | V | W | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.035928 | 0.007984 | 0.041916 | 0.131737 | 0.055888 | 0.049900 | 0.017964 | 0.081836 | 0.119760 | 0.107784 | 0.015968 | 0.037924 | 0.037924 | 0.011976 | 0.037924 | 0.055888 | 0.049900 | 0.057884 | 0.013972 | 0.029940 |
| 1 | 0.076233 | 0.004484 | 0.049327 | 0.065770 | 0.029895 | 0.082212 | 0.020927 | 0.055306 | 0.082212 | 0.074738 | 0.040359 | 0.037369 | 0.043348 | 0.056801 | 0.058296 | 0.055306 | 0.061286 | 0.053812 | 0.017937 | 0.034380 |
| 1 | 0.093333 | 0.009524 | 0.068571 | 0.080000 | 0.026667 | 0.120000 | 0.024762 | 0.059048 | 0.055238 | 0.095238 | 0.028571 | 0.015238 | 0.041905 | 0.019048 | 0.074286 | 0.060952 | 0.020952 | 0.053333 | 0.009524 | 0.043810 |
| 1 | 0.079470 | 0.036424 | 0.052980 | 0.067881 | 0.046358 | 0.072848 | 0.023179 | 0.046358 | 0.021523 | 0.117550 | 0.019868 | 0.016556 | 0.046358 | 0.039735 | 0.081126 | 0.072848 | 0.049669 | 0.072848 | 0.008278 | 0.028146 |
| 1 | 0.084158 | 0.003300 | 0.046205 | 0.094059 | 0.034653 | 0.077558 | 0.018152 | 0.061056 | 0.089109 | 0.099010 | 0.036304 | 0.057756 | 0.031353 | 0.029703 | 0.026403 | 0.047855 | 0.042904 | 0.061056 | 0.011551 | 0.047855 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| -1 | 0.087221 | 0.004057 | 0.050710 | 0.060852 | 0.034483 | 0.068966 | 0.020284 | 0.056795 | 0.070994 | 0.089249 | 0.020284 | 0.036511 | 0.050710 | 0.042596 | 0.054767 | 0.079108 | 0.052738 | 0.075051 | 0.004057 | 0.040568 |
| -1 | 0.067901 | 0.009259 | 0.049383 | 0.030864 | 0.027778 | 0.055556 | 0.024691 | 0.037037 | 0.030864 | 0.080247 | 0.015432 | 0.040123 | 0.111111 | 0.080247 | 0.104938 | 0.101852 | 0.058642 | 0.030864 | 0.018519 | 0.024691 |
| -1 | 0.053521 | 0.010329 | 0.056338 | 0.101408 | 0.037559 | 0.037559 | 0.014085 | 0.059155 | 0.082629 | 0.110798 | 0.025352 | 0.059155 | 0.029108 | 0.047887 | 0.061033 | 0.078873 | 0.048826 | 0.046948 | 0.005634 | 0.033803 |
| -1 | 0.038462 | 0.022869 | 0.070686 | 0.062370 | 0.062370 | 0.024948 | 0.014553 | 0.066528 | 0.060291 | 0.121622 | 0.016632 | 0.069647 | 0.027027 | 0.040541 | 0.050936 | 0.096674 | 0.061331 | 0.058212 | 0.009356 | 0.024948 |
| -1 | 0.042791 | 0.014884 | 0.055814 | 0.071628 | 0.058605 | 0.032558 | 0.020465 | 0.053953 | 0.071628 | 0.110698 | 0.010233 | 0.054884 | 0.044651 | 0.042791 | 0.059535 | 0.102326 | 0.040930 | 0.054884 | 0.013023 | 0.043721 |
234 rows × 20 columns
Next, we’ll check how these different amino acid compositions are correlated in our dataset. The pairwise correlations will be calculated using the coor function from the pandas library and the ploting is done using the heatmap function of the seaborn library.
df1.corr()
| A | C | D | E | F | G | H | I | K | L | M | N | P | Q | R | S | T | V | W | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1.000000 | -0.184260 | 0.177636 | -0.057060 | -0.428029 | 0.535464 | 0.026502 | -0.535485 | -0.601721 | -0.056621 | 0.109226 | -0.614635 | 0.302125 | -0.078730 | 0.441783 | -0.371119 | 0.035769 | 0.326958 | 0.011428 | -0.439110 |
| C | -0.184260 | 1.000000 | -0.192868 | -0.242481 | 0.094535 | -0.081970 | 0.259811 | -0.105199 | -0.092816 | 0.114812 | -0.049184 | 0.011896 | -0.004548 | 0.044336 | -0.062432 | 0.258855 | 0.139419 | 0.055470 | 0.106561 | -0.130594 |
| D | 0.177636 | -0.192868 | 1.000000 | 0.085949 | -0.052983 | 0.069555 | -0.109608 | -0.098274 | -0.121791 | -0.302167 | 0.115397 | -0.128898 | -0.148293 | -0.099212 | 0.085597 | -0.186648 | -0.074650 | 0.121422 | -0.088707 | 0.039454 |
| E | -0.057060 | -0.242481 | 0.085949 | 1.000000 | -0.078805 | -0.111516 | -0.186326 | -0.073880 | 0.157472 | -0.012459 | 0.129350 | -0.237316 | -0.104275 | -0.287366 | 0.226413 | -0.364977 | -0.294016 | 0.126782 | -0.062614 | -0.029676 |
| F | -0.428029 | 0.094535 | -0.052983 | -0.078805 | 1.000000 | -0.410708 | 0.015082 | 0.219202 | 0.288150 | 0.046775 | -0.124937 | 0.286611 | -0.268231 | 0.020734 | -0.323619 | 0.191448 | -0.148088 | -0.198901 | 0.008206 | 0.256438 |
| G | 0.535464 | -0.081970 | 0.069555 | -0.111516 | -0.410708 | 1.000000 | 0.005153 | -0.344833 | -0.515264 | -0.259590 | 0.116196 | -0.498443 | 0.400449 | -0.150103 | 0.282059 | -0.290522 | -0.029106 | 0.326405 | 0.045311 | -0.253129 |
| H | 0.026502 | 0.259811 | -0.109608 | -0.186326 | 0.015082 | 0.005153 | 1.000000 | -0.191350 | -0.251606 | -0.029982 | -0.002517 | -0.130458 | 0.193951 | 0.010474 | 0.194649 | 0.058559 | -0.011848 | 0.024193 | 0.234194 | -0.077898 |
| I | -0.535485 | -0.105199 | -0.098274 | -0.073880 | 0.219202 | -0.344833 | -0.191350 | 1.000000 | 0.564864 | -0.097153 | -0.107219 | 0.652231 | -0.500893 | -0.135589 | -0.549266 | 0.018739 | -0.115790 | -0.355284 | -0.287326 | 0.399591 |
| K | -0.601721 | -0.092816 | -0.121791 | 0.157472 | 0.288150 | -0.515264 | -0.251606 | 0.564864 | 1.000000 | -0.083722 | -0.058253 | 0.596283 | -0.426019 | -0.058201 | -0.658596 | 0.015579 | -0.132401 | -0.357959 | -0.231120 | 0.392476 |
| L | -0.056621 | 0.114812 | -0.302167 | -0.012459 | 0.046775 | -0.259590 | -0.029982 | -0.097153 | -0.083722 | 1.000000 | -0.210467 | -0.007216 | -0.131931 | 0.086540 | 0.101612 | 0.120448 | -0.068529 | -0.196288 | -0.066282 | -0.132099 |
| M | 0.109226 | -0.049184 | 0.115397 | 0.129350 | -0.124937 | 0.116196 | -0.002517 | -0.107219 | -0.058253 | -0.210467 | 1.000000 | -0.166302 | 0.010506 | 0.049905 | 0.141045 | -0.180492 | -0.125789 | -0.068954 | -0.041573 | -0.083172 |
| N | -0.614635 | 0.011896 | -0.128898 | -0.237316 | 0.286611 | -0.498443 | -0.130458 | 0.652231 | 0.596283 | -0.007216 | -0.166302 | 1.000000 | -0.477939 | 0.046522 | -0.628771 | 0.248356 | 0.008508 | -0.443414 | -0.212952 | 0.403479 |
| P | 0.302125 | -0.004548 | -0.148293 | -0.104275 | -0.268231 | 0.400449 | 0.193951 | -0.500893 | -0.426019 | -0.131931 | 0.010506 | -0.477939 | 1.000000 | 0.132678 | 0.357570 | -0.123427 | 0.041728 | 0.128161 | 0.328047 | -0.266483 |
| Q | -0.078730 | 0.044336 | -0.099212 | -0.287366 | 0.020734 | -0.150103 | 0.010474 | -0.135589 | -0.058201 | 0.086540 | 0.049905 | 0.046522 | 0.132678 | 1.000000 | -0.054100 | 0.200578 | 0.132633 | -0.315732 | -0.052772 | -0.120306 |
| R | 0.441783 | -0.062432 | 0.085597 | 0.226413 | -0.323619 | 0.282059 | 0.194649 | -0.549266 | -0.658596 | 0.101612 | 0.141045 | -0.628771 | 0.357570 | -0.054100 | 1.000000 | -0.201870 | -0.176378 | 0.251911 | 0.185710 | -0.339511 |
| S | -0.371119 | 0.258855 | -0.186648 | -0.364977 | 0.191448 | -0.290522 | 0.058559 | 0.018739 | 0.015579 | 0.120448 | -0.180492 | 0.248356 | -0.123427 | 0.200578 | -0.201870 | 1.000000 | 0.238065 | -0.204485 | 0.016755 | -0.008286 |
| T | 0.035769 | 0.139419 | -0.074650 | -0.294016 | -0.148088 | -0.029106 | -0.011848 | -0.115790 | -0.132401 | -0.068529 | -0.125789 | 0.008508 | 0.041728 | 0.132633 | -0.176378 | 0.238065 | 1.000000 | 0.016057 | 0.027796 | -0.227650 |
| V | 0.326958 | 0.055470 | 0.121422 | 0.126782 | -0.198901 | 0.326405 | 0.024193 | -0.355284 | -0.357959 | -0.196288 | -0.068954 | -0.443414 | 0.128161 | -0.315732 | 0.251911 | -0.204485 | 0.016057 | 1.000000 | 0.093460 | -0.245204 |
| W | 0.011428 | 0.106561 | -0.088707 | -0.062614 | 0.008206 | 0.045311 | 0.234194 | -0.287326 | -0.231120 | -0.066282 | -0.041573 | -0.212952 | 0.328047 | -0.052772 | 0.185710 | 0.016755 | 0.027796 | 0.093460 | 1.000000 | 0.067800 |
| Y | -0.439110 | -0.130594 | 0.039454 | -0.029676 | 0.256438 | -0.253129 | -0.077898 | 0.399591 | 0.392476 | -0.132099 | -0.083172 | 0.403479 | -0.266483 | -0.120306 | -0.339511 | -0.008286 | -0.227650 | -0.245204 | 0.067800 | 1.000000 |
#correlation between different features
sns.heatmap(df1.corr())
<Axes: >

Model building#
Now, we’ll split our data into training and testing sub-sets. The training set will be used to build the SVM model and the testing set will be used to test the accuracy of the model. The train_test_split function in model_selection is used to create these sub-set given the data matrix (X) and labels (Y). For this function, the test_size keyword argument determines the size for the training and testing sub-set. E.g., when test_size is set to 0.2 then this imply that the model training will be done using 80% of the data and testing will be performed using the remaining 20% of the data. This approach ensures that when we are test our model, we are using data that has not been used for training the model. Subsequently, we’ll build the SVM model using the training dataset and check its prediction accuracy using the testing dataset.
x = df1.values
print(x)
[[0.03592814 0.00798403 0.04191617 ... 0.05788423 0.01397206 0.02994012]
[0.07623318 0.0044843 0.04932735 ... 0.05381166 0.01793722 0.03437967]
[0.09333333 0.00952381 0.06857143 ... 0.05333333 0.00952381 0.04380952]
...
[0.05352113 0.01032864 0.05633803 ... 0.04694836 0.0056338 0.03380282]
[0.03846154 0.02286902 0.07068607 ... 0.05821206 0.00935551 0.02494802]
[0.0427907 0.01488372 0.05581395 ... 0.05488372 0.01302326 0.04372093]]
y_labels = df1.index.values.astype(int)
y_labels
array([ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1])
# Split-out validation dataset"
validation_size = 0.20 # 20% data for testing
seed = None # change to int for reproducibility
X_train, X_validation, Y_train, Y_validation = model_selection.train_test_split(df1, y_labels, \
test_size=validation_size, \
random_state=seed)
new_clf = SVC()
model1 = new_clf.fit(X_train, Y_train)
Y_predicted = model1.predict(X_validation)
score1 = accuracy_score(Y_predicted, Y_validation)
print(score1)
0.7659574468085106
y_labels
array([ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1])
Cross-validation#
One of the limitation of the approach used above is that we are not using the entire data for model building since a sub-set of data is set aside for testing. To overcome this limitation, the cross-validation approach is used. Here, multiple splits of the data are created and each of these splits are iteratively used for model building and testing. This way we have practically used the entire data for model building. This method is called kfold cross validation, where k indicates the number of splits.
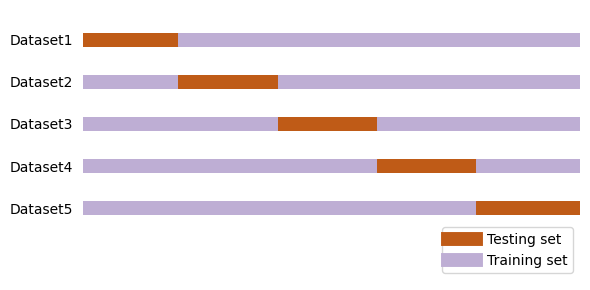
The cross_val_score function in model.selection class is used to perform the kfold cross validation by specifying the required value to the cv keyword argument.
# Test options and evaluation metric
scoring = 'accuracy'
kfold = model_selection.KFold(n_splits=10)
cv_results = model_selection.cross_val_score(SVC(), df1, y_labels, cv=kfold, scoring=scoring)
print(cv_results)
print(cv_results.mean(), cv_results.std())
[0.54166667 0.625 0.5 0.83333333 0.60869565 0.69565217
0.43478261 0.56521739 0.73913043 0.60869565]
0.6152173913043478 0.11104998581213907
SVC().get_params()
{'C': 1.0,
'break_ties': False,
'cache_size': 200,
'class_weight': None,
'coef0': 0.0,
'decision_function_shape': 'ovr',
'degree': 3,
'gamma': 'scale',
'kernel': 'rbf',
'max_iter': -1,
'probability': False,
'random_state': None,
'shrinking': True,
'tol': 0.001,
'verbose': False}
Hyperparameters#
clf_poly = SVC(kernel='poly', degree=3)
clf_rbf = SVC(kernel='rbf', C=10)
kfold = model_selection.KFold(n_splits=10)
cv_SVM_poly_results = model_selection.cross_val_score(clf_poly, df1, y_labels, cv=kfold, scoring=scoring)
cv_SVM_rbf_results = model_selection.cross_val_score(clf_rbf, df1, y_labels, cv=kfold, scoring=scoring)
print(cv_SVM_rbf_results)
print (cv_SVM_poly_results.mean(), cv_SVM_rbf_results.mean())
[0.66666667 0.79166667 0.79166667 0.91666667 0.7826087 0.69565217
0.60869565 0.69565217 0.7826087 0.82608696]
0.7215579710144928 0.7557971014492753
Grid Search#
from sklearn.model_selection import GridSearchCV
tuned_parameters = [{'kernel': ['rbf'], 'gamma': [1e-3, 1e-4],
'C': [1, 10, 100, 1000, 10000]},
{'kernel': ['linear'], 'C': [1, 10, 100, 1000, 10000]},
{'kernel':['poly'], 'C': [1, 10, 100, 1000, 10000],
'degree': range(10)}]
clf_grid = GridSearchCV(SVC(), tuned_parameters, cv=10, scoring='accuracy')
clf_grid.fit(df1,y_labels)
GridSearchCV(cv=10, estimator=SVC(),
param_grid=[{'C': [1, 10, 100, 1000, 10000],
'gamma': [0.001, 0.0001], 'kernel': ['rbf']},
{'C': [1, 10, 100, 1000, 10000], 'kernel': ['linear']},
{'C': [1, 10, 100, 1000, 10000],
'degree': range(0, 10), 'kernel': ['poly']}],
scoring='accuracy')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GridSearchCV(cv=10, estimator=SVC(),
param_grid=[{'C': [1, 10, 100, 1000, 10000],
'gamma': [0.001, 0.0001], 'kernel': ['rbf']},
{'C': [1, 10, 100, 1000, 10000], 'kernel': ['linear']},
{'C': [1, 10, 100, 1000, 10000],
'degree': range(0, 10), 'kernel': ['poly']}],
scoring='accuracy')SVC()
SVC()
print(clf_grid.best_params_)
#print(clf_grid.cv_results_)
{'C': 10, 'degree': 2, 'kernel': 'poly'}
Build a SVM model using above hyperparameters and check the prediction accuracy.
clf_poly = SVC(C=10, degree=2, kernel='poly')
kfold = model_selection.KFold(n_splits=10)
cv_SVM_results = model_selection.cross_val_score(clf_poly, df1, y_labels, cv=kfold, scoring=scoring)
print(cv_SVM_results)
print (cv_SVM_results.mean(),cv_SVM_results.std())
[0.70833333 0.70833333 0.75 0.875 0.73913043 0.65217391
0.65217391 0.60869565 0.7826087 0.82608696]
0.7302536231884058 0.07827868993299868
# To predict class for a new protein pass its
# amino-acid composition as an arugument to predict function.
clf_poly.predict([])
Confusion matrix#
from collections import Counter
from sklearn.metrics import confusion_matrix, classification_report
kfold = model_selection.KFold(n_splits=10)
cv_results = model_selection.cross_val_predict(SVC(kernel='poly',degree=2, C=10), df1, y_labels, cv=kfold)
score1 = accuracy_score(cv_results, y_labels)
print(score1)
0.7307692307692307
print(Counter(y_labels))
print(Counter(cv_results))
Counter({1: 117, -1: 117})
Counter({1: 122, -1: 112})
cm = confusion_matrix(y_labels,cv_results)
print(cm)
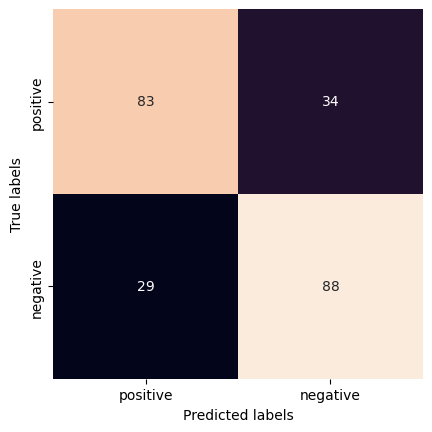
fig,ax= plt.subplots()
sns.heatmap(cm, square=True, annot=True, fmt='g', cbar=False, ax=ax)
ax.set_xlabel('Predicted labels')
ax.set_ylabel('True labels')
ax.xaxis.set_ticklabels(['positive', 'negative'])
ax.yaxis.set_ticklabels(['positive', 'negative'])
plt.show()
[[83 34]
[29 88]]
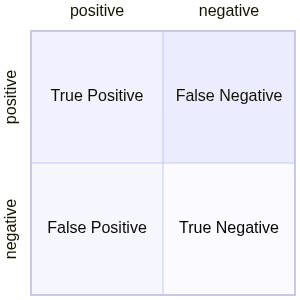
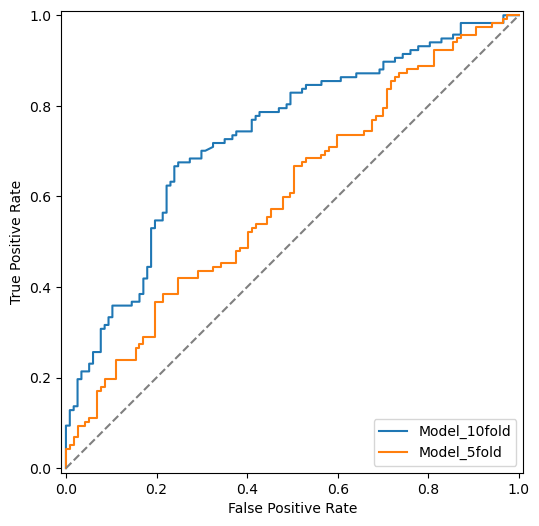
ROC Curve#
Build two models - one with 5-fold CV and another with 10-fold CV. Both model should have probabilities for each class.
kfold = model_selection.KFold(n_splits=10)
cv_results_prob = model_selection.cross_val_predict(SVC(kernel='poly',degree=2, C=10, probability=True), df1, y_labels, cv=kfold, method='predict_proba')
kfold = model_selection.KFold(n_splits=5)
cv_results_prob_5 = model_selection.cross_val_predict(SVC(kernel='poly',degree=3, probability=True), df1, y_labels, cv=kfold, method='predict_proba')
from sklearn.metrics import roc_curve
from sklearn.metrics import RocCurveDisplay
fig, ax = plt.subplots(figsize=(6, 6))
fpr, tpr, _ = roc_curve(y_labels, cv_results_prob[:, 1])
roc_display = RocCurveDisplay(fpr=fpr, tpr=tpr, estimator_name="Model_10fold").plot(ax=ax)
fpr, tpr, _ = roc_curve(y_labels, cv_results_prob_5[:, 1])
roc_display2 = RocCurveDisplay(fpr=fpr, tpr=tpr, estimator_name="Model_5fold").plot(ax=ax)
plt.plot([0, 1], [0, 1], color = 'grey', linestyle="dashed")
plt.show()
Statistical analysis#
kfold = model_selection.KFold(n_splits=10)
cv_new_predict = model_selection.cross_val_predict(SVC(kernel='poly',degree=3, C=10), df1, y_labels, cv=kfold)
cv_new_predict
array([-1, 1, 1, -1, -1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1,
1, -1, 1, 1, -1, 1, 1, -1, 1, 1, 1, 1, 1, -1, 1, 1, 1,
1, 1, 1, 1, 1, 1, -1, 1, -1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, -1, -1, 1, 1, 1, 1, 1, -1, 1, 1, -1, 1,
-1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, -1, 1, 1, -1, 1, 1,
-1, -1, 1, 1, -1, 1, 1, 1, 1, -1, 1, -1, 1, 1, 1, 1, 1,
1, -1, 1, 1, -1, -1, -1, -1, 1, -1, 1, 1, 1, 1, 1, -1, -1,
1, 1, -1, 1, 1, 1, -1, 1, 1, -1, -1, -1, 1, -1, -1, -1, 1,
-1, -1, 1, -1, 1, -1, 1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1,
-1, 1, -1, 1, 1, 1, 1, 1, 1, 1, -1, -1, -1, 1, 1, -1, -1,
-1, 1, -1, -1, -1, -1, 1, 1, -1, 1, 1, -1, -1, -1, 1, 1, -1,
-1, 1, 1, -1, -1, 1, 1, -1, -1, -1, 1, -1, -1, -1, -1, 1, 1,
-1, -1, -1, -1, 1, -1, 1, 1, -1, 1, -1, -1, 1, -1, 1, -1, -1,
-1, 1, -1, -1, -1, -1, -1, -1, 1, 1, -1, -1, -1])
from sklearn.metrics import classification_report
print(classification_report(y_labels, cv_new_predict))
precision recall f1-score support
-1 0.69 0.57 0.63 117
1 0.64 0.74 0.69 117
accuracy 0.66 234
macro avg 0.66 0.66 0.66 234
weighted avg 0.66 0.66 0.66 234
from sklearn.metrics import roc_auc_score
auc_10 = roc_auc_score(y_labels, cv_results_prob[:, 1])
print(f"10-Fold CV AUC: {auc_10:.4f}")
# AUC for 5-fold CV
auc_5 = roc_auc_score(y_labels, cv_results_prob_5[:, 1])
print(f"5-Fold CV AUC: {auc_5:.4f}")
10-Fold CV AUC: 0.7339
5-Fold CV AUC: 0.6000
Exercise#
Extract another feature - Di-Peptide Composition (DPC)
For each sequence calculate the frequency of pairwaise occurrence of amino acids. The length of the feature vector for each sequence would be 400 (20 x 20). Construct a classification model using DPC as a feature and compare the results with classification using amino acid composition.
“ACDFERDFERALK” 20x20
import itertools
aa_list = ['A','C','D','E','F','G','H','I','K','L','M','N','P','Q','R','S','T','V','W','Y']
## Create a series of dipeptides
dpc_series = pd.Series(name='1',dtype=float)
for x in itertools.product(aa_list,aa_list):
dpc_series[''.join([''.join(x)])] = 0
dpc_series
AA 0
AC 0
AD 0
AE 0
AF 0
..
YS 0
YT 0
YV 0
YW 0
YY 0
Name: 1, Length: 400, dtype: int64
df_dpc = pd.DataFrame([])
for keys,values in positive_dict.items():
dpc_series_copy = dpc_series.copy()
# print (values.seq)
dpc_seq = [str(values.seq[i:i+2]) for i in range(len(values.seq))]
del dpc_seq[-1]
for x in dpc_seq:
dpc_series_copy[x] += 1
dpc_series_copy /= len(values.seq)
dpc_series_copy *= 100
# df_dpc = df_dpc.append(dpc_series_copy)
df_dpc = pd.concat([df_dpc, dpc_series_copy], axis=1)
df_dpc.T
| AA | AC | AD | AE | AF | AG | AH | AI | AK | AL | ... | YM | YN | YP | YQ | YR | YS | YT | YV | YW | YY | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.399202 | 0.000000 | 0.000000 | 0.399202 | 0.399202 | 0.399202 | 0.199601 | 0.199601 | 0.598802 | 0.199601 | ... | 0.199601 | 0.000000 | 0.598802 | 0.199601 | 0.000000 | 0.199601 | 0.000000 | 0.000000 | 0.0 | 0.000000 |
| 1 | 1.345291 | 0.000000 | 0.149477 | 0.747384 | 0.149477 | 0.597907 | 0.149477 | 0.298954 | 0.896861 | 0.448430 | ... | 0.000000 | 0.000000 | 0.298954 | 0.448430 | 0.000000 | 0.000000 | 0.298954 | 0.597907 | 0.0 | 0.000000 |
| 1 | 0.571429 | 0.000000 | 0.761905 | 0.761905 | 0.380952 | 1.142857 | 0.190476 | 0.380952 | 0.571429 | 1.142857 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.761905 | 0.190476 | 0.190476 | 0.190476 | 0.0 | 0.000000 |
| 1 | 0.331126 | 0.165563 | 0.331126 | 0.496689 | 0.662252 | 0.662252 | 0.331126 | 0.000000 | 0.165563 | 0.496689 | ... | 0.000000 | 0.165563 | 0.165563 | 0.331126 | 0.827815 | 0.331126 | 0.000000 | 0.165563 | 0.0 | 0.000000 |
| 1 | 0.495050 | 0.000000 | 0.660066 | 0.990099 | 0.165017 | 0.660066 | 0.000000 | 0.165017 | 0.825083 | 0.825083 | ... | 0.165017 | 0.495050 | 0.165017 | 0.165017 | 0.165017 | 0.165017 | 0.165017 | 0.330033 | 0.0 | 0.330033 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 1 | 0.790514 | 0.000000 | 0.592885 | 0.395257 | 0.592885 | 0.592885 | 0.197628 | 0.197628 | 1.185771 | 0.395257 | ... | 0.000000 | 0.000000 | 0.197628 | 0.000000 | 0.395257 | 0.197628 | 0.000000 | 0.000000 | 0.0 | 0.000000 |
| 1 | 0.401606 | 0.000000 | 0.401606 | 0.200803 | 1.004016 | 0.200803 | 0.401606 | 0.000000 | 0.803213 | 0.200803 | ... | 0.000000 | 0.000000 | 0.000000 | 0.401606 | 0.200803 | 0.602410 | 0.200803 | 0.803213 | 0.0 | 0.401606 |
| 1 | 2.923977 | 0.000000 | 1.754386 | 1.949318 | 1.169591 | 0.779727 | 0.194932 | 0.389864 | 0.000000 | 1.559454 | ... | 0.000000 | 0.000000 | 0.194932 | 0.000000 | 0.584795 | 0.000000 | 0.000000 | 0.000000 | 0.0 | 0.000000 |
| 1 | 0.000000 | 0.000000 | 0.114416 | 0.114416 | 0.114416 | 0.114416 | 0.114416 | 0.114416 | 0.343249 | 0.114416 | ... | 0.000000 | 0.228833 | 0.228833 | 0.000000 | 0.228833 | 0.228833 | 0.228833 | 0.228833 | 0.0 | 0.228833 |
| 1 | 0.000000 | 0.142653 | 0.285307 | 0.000000 | 0.570613 | 0.000000 | 0.285307 | 0.855920 | 0.570613 | 1.711840 | ... | 0.000000 | 0.000000 | 0.142653 | 0.427960 | 0.000000 | 0.000000 | 0.142653 | 0.000000 | 0.0 | 0.285307 |
117 rows × 400 columns
